https://doi.org/10.7343/as-2022-692
Improved groundwater modeling by incorporating geological information from hydrogeological sections
Submitted: 21 June 2023
Accepted: 6 November 2023
Published: 14 November 2023
Accepted: 6 November 2023
Abstract Views: 393
PDF: 310
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Authors
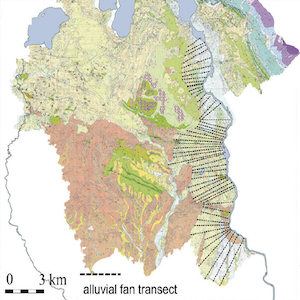
Geological cross-sections are usually employed in the hydrogeological model conceptualization, but their usage may not be easily exploited in subsequent modeling phases. The spatial distribution of geological facies along a geological section’s track may significantly vary when using random facies fields, and these may not be faithful to the original conceptualization described by the geological section. The present work offers a novel framework for improving available hydrogeological models using geological sections as a more quantitative source of information, hence by taking into account of information coming from a geological section. Then, this information given by the change in the distribution of porosities is transferred from the section’s track to surrounding locations through a proper kriging procedure upon a chosen Correlation Scale (R), which is exponentially correlated in space. This procedure is tested by using porosity distributions upon several R, associating a conductivity value with each porosity one through empirical formulations, and informing several numerical models related to a real case study (an aquifer in the province of Lecco, Northern Italy). The proposed procedure enables to significantly outperform the former calibrated numerical model. Best-calibrated models show that the convenient R could be from 2 to 5 kilometers long, consistent with the width of the alluvial and fluvioglacial floodplain that characterizes the aquifer under examination.
Beretta, G. P., Denti, E., Francani, V., and Sala, P. Lineamenti idrogeologici del settore 393 sublacquale della provincia di Como. Acque Sotterranee, a. 1, n. 4, p. 23-62, December 1984.
Bianchi-Janetti, E., Guadagnini, L., Riva, M., and Guadagnini, A. Global sensitivity analyses of multiple conceptual models with uncertain parameters driving groundwater flow in a regional-scale sedimentary aquifer. Journal of Hydrology. https://doi.org/10.1016/j.jhydrol.2019.04.035.
DOI: https://doi.org/10.1016/j.jhydrol.2019.04.035
Carman, P.C., 1956. Flow of gases through porous media. Butterworths Scientific Publications, London.
Cavallin A., Francani V., Mazzarella S., 1983. Studio idrogeologico della pianura compresa tra Adda e Ticino, CAP Milano.
Chiles, J. P., & Delfiner, P. (2009). Geostatistics: Modeling spatial uncertainty (Vol. 497).
Deutsch, C.V. and Journel, A.G., (1997). GSLIB Geostatistical Software Library and User’s Guide, Oxford University Press, New York, second edition. 369 pages.
Fontana, A., Mozzi, P., and Marchetti, M., 2014. Alluvial fans and megafans along the southern side of the Alps. Sedimentary Geology 301, 150–171. http://dx.doi.org/10.1016/j.sedgeo.2013.09.003.
DOI: https://doi.org/10.1016/j.sedgeo.2013.09.003
Freeze, R. A., and Cherry, J. A. Groundwater. Englewood Cliffs, N.J: Prentice-Hall, 1979. Print.
Goovaerts, P. (1997). Geostatistics for natural resources evaluation. Oxford University Press, New York
DOI: https://doi.org/10.1093/oso/9780195115383.001.0001
Guadagnini, L., Guadagnini, A., Tartakovsky, D.M., 2004. Probabilistic reconstruction of geologic facies. J. Hydrol. 294, 57–67. https://doi.org/10.1016/j.jhydrol.2004.02.007.
DOI: https://doi.org/10.1016/j.jhydrol.2004.02.007
Gueting, N., Caers, J., Comunian, A. et al. Reconstruction of Three-Dimensional Aquifer Heterogeneity from Two-Dimensional Geophysical Data. Math Geosci 50, 53–75 (2018). https://doi.org/10.1007/s11004-017-9694-x
DOI: https://doi.org/10.1007/s11004-017-9694-x
Isaaks, E. H., and Srivastava, R. M. Applied Geostatistics. New York, Oxford University press, 1989.
Jorreto-Zaguirre, S., Dowd, P. A., Pardo-Igúzquiza, E., Pulido-Bosch, A., and Sánchez-Martos, F., 2020. Stochastic Simulation of the Spatial Heterogeneity of Deltaic Facies Accounting for the Uncertainty of Facies Proportions. Frontiers Earth Science 8, 563122. https://doi: 10.3389/feart.2020.563122.
DOI: https://doi.org/10.3389/feart.2020.563122
Kozeny, J., 1927 Uber kapillare leitung des wassers im boden: Sitzungsber [On capillary flow of water in soil], vol 136. Sitz Ber Akad Wiss Wien, Vienna, pp 271–306.
Remy, N., Boucher, A., and Wu, J. (2009). Applied geostatistics with SGeMS: a user’s guide. Cambridge University Press, New York
DOI: https://doi.org/10.1017/CBO9781139150019
Riva, M., Guadagnini, A., Fernandez-Garcia, D., Sanchez-Vila, X., Ptak, T., 2008. Relative importance of geostatistical and transport models in describing heavily tailed breakthrough curves at the Lauswiesen site. J Contam Hydrol 101:1–13.
DOI: https://doi.org/10.1016/j.jconhyd.2008.07.004
Riva, M., Guadagnini, L., and Guadagnini, A., 2010. Effects of uncertainty of lithofacies, conductivity and porosity distributions on stochastic interpretations of a field scale tracer test. Stoch Environ Res Risk Assess 24, 955–970. https://doi.org/10.1007/s00477-010-0399-7
DOI: https://doi.org/10.1007/s00477-010-0399-7
Riva, M., Guadagnini, L., Guadagnini, A., Ptak, T., and Martac, E., 2006. Probabilistic study of well capture zones distribution at the Lauswiesen field site. J. Contam. Hydrol., 88(1-2), 92-118, doi:10.1016/j.jconhyd.2006.06.005
DOI: https://doi.org/10.1016/j.jconhyd.2006.06.005
Rojas, R., Feyen, L., and Dassargues, A., 2008. Conceptual model uncertainty in groundwater modeling: Combining generalized likelihood uncertainty estimation and Bayesian model averaging, Water Resour. Res., 44, W12418, doi:10.1029/2008WR006908.
DOI: https://doi.org/10.1029/2008WR006908
Rosas, J., Lopez, O., Missimer, T. M., Coulibaly, K. M., Dehwah, A. ,Sesler, K., Lujan, L. R., and Mantilla, D. (2014) Determination of hydraulic conductivity from grain-size distribution for different depositional environments. Ground Water 52(3):399—413.doi: https://doi.org/10.1111/gwat.12078
DOI: https://doi.org/10.1111/gwat.12078
Schiavo, M., 2022. Probabilistic delineation of subsurface connected pathways in alluvial aquifers under geological uncertainty. Journal of Hydrology 614 B (2022), https://doi.org/10.1016/j.jhydrol.2022.128674
DOI: https://doi.org/10.1016/j.jhydrol.2022.128674
Schiavo, M., 2023. The role of different sources of uncertainty on the stochastic quantification of subsurface discharges in heterogeneous aquifers. Journal of Hydrology, Volume 617, Part B, February 2023, 128930. https://doi.org/10.1016/j.jhydrol.2022.128930
DOI: https://doi.org/10.1016/j.jhydrol.2022.128930
Schiavo, M., Riva, M., Guadagnini, L., Zehe, E., and Guadagnini, A., 2022. Probabilistic identification of Preferential Groundwater Networks. Journal of Hydrology 610 (2022) 127906. https://doi.org/10.1016/j.jhydrol.2022.127906
DOI: https://doi.org/10.1016/j.jhydrol.2022.127906
Schorpp, L., Straubhaar, J., and Renard. P. (2022). Automated Hierarchical 3D Modeling of Quaternary Aquifers: The ArchPy Approach. Front. Earth Sci. 10:884075. doi: 10.3389/feart.2022.884075.
DOI: https://doi.org/10.3389/feart.2022.884075
Siena, M., and Riva, M. Impact of geostatistical reconstruction approaches on model calibration for flow in highly heterogeneous aquifers. Stoch Environ Res Risk Assess 34, 1591–1606 (2020). https://doi.org/10.1007/s00477-020-01865-2
DOI: https://doi.org/10.1007/s00477-020-01865-2
Vukovic, M., and Soro, A., 1992. Hydraulics and water wells: theory and application. Water Resources Publications, Highlands Ranch, CO, USA. 1143 Hydrogeology
How to Cite
Schiavo, M. (2023). Improved groundwater modeling by incorporating geological information from hydrogeological sections. Acque Sotterranee - Italian Journal of Groundwater, 12(4), 9–17. https://doi.org/10.7343/as-2022-692
Copyright (c) 2023 the Author(s)
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
PAGEPress has chosen to apply the Creative Commons Attribution NonCommercial 4.0 International License (CC BY-NC 4.0) to all manuscripts to be published.
Similar Articles
- Francesca Lotti, Antonella Baiocchi, Salvatore D'Onofrio, Vincenzo Piscopo, Hydrogeological site characterization of marly-silici-calcareous rocks through surveys of discontinuities and pumping tests , Acque Sotterranee - Italian Journal of Groundwater: Vol. 1 No. 1 (2012)
- Marco Amanti, Giovanni Conte, Lucio Martarelli, Gennaro Maria Monti, Guido Motteran, Anna Rosa Scalise, Roberto Serafini, Angelantonio Silvi, Hydrogeological map of Italy: the preliminary Sheet N. 348 Antrodoco (Central Italy) , Acque Sotterranee - Italian Journal of Groundwater: Vol. 5 No. 2 (2016)
- Stefano Viaroli, Lucia Mastrorillo, Roberto Mazza, Vittorio Paolucci, Hydrostructural setting of Riardo Plain: effects on Ferrarelle mineral water type , Acque Sotterranee - Italian Journal of Groundwater: Vol. 5 No. 3 (2016)
- Mariachiara Caschetto, Ammonium natural attenuation in complex hydrogeological settings: insights from a multi-isotope approach , Acque Sotterranee - Italian Journal of Groundwater: Vol. 6 No. 4 (2017)
- Leonardo Piccinini, Valentina Vincenzi, Alessandro Pontin, Federico Tonet, Heat transport modeling for the design of a low enthalpy open-loop system , Acque Sotterranee - Italian Journal of Groundwater: Vol. 1 No. 3 (2012)
- Behailu Birhanu, Seifu Kebede, Marco Masetti, Tenalem Ayenew, WEAP-MODFLOW dynamic modeling approach to evaluate surface water and groundwater supply sources of Addis Ababa city , Acque Sotterranee - Italian Journal of Groundwater: Vol. 7 No. 2 (2018)
- Matia Menichini, Marco Doveri, Leonardo Piccini, Hydrogeological and geochemical overview of the karst aquifers in the Apuan Alps (Northwestern Tuscany, Italy) , Acque Sotterranee - Italian Journal of Groundwater: Vol. 5 No. 1 (2016)
- Giorgia Lucianetti, Lucia Mastrorillo, Roberto Mazza, Preliminary conceptual model of an Alpine carbonate aquifer (Pale di San Martino, Dolomites, Italy) , Acque Sotterranee - Italian Journal of Groundwater: Vol. 5 No. 2 (2016)
- Giuseppe Sappa, Flavia Ferranti, Francesco Maria De Filippi, A proposal of conceptual model for Pertuso Spring discharge evaluation in the Upper Valley of Aniene River , Acque Sotterranee - Italian Journal of Groundwater: Vol. 5 No. 3 (2016)
- Antonio Dematteis, Piergiuseppe Gilli, Maria Elena Parisi, Lorenzo Ferrero, Fabio Furno, Maddalena exploratory adit: feedback on hydrogeological and geothermal aspects , Acque Sotterranee - Italian Journal of Groundwater: Vol. 5 No. 4 (2016)
You may also start an advanced similarity search for this article.
